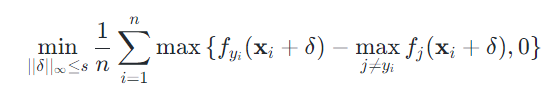Zeroth order Attack

Source Code:

Deep Neural Networks (DNNs) have made many breakthroughs in different areas of AI such as image classification, object detection and speech recognition. However, recent studies have shown that DNNs are vulnerable to adversarial examples. Adversarial examples represent slightly modified data to which a tiny perturbation is applied. This perturbation is almost imperceptible for a human but that could deceive even a well-trained DNN, pushing it to misclassify the label of the data. Depending on how much information is available to an attacker, it is possible to classify adversarial attacks into two classes: white box attack, where the adversary has full access to the target model, and black-box attack where the attacker does not have full access to the target model. In particular, in the white-box setting the attacker knows the model architecture, the parameters, inputs and outputs and it can query the model and calculate the gradient. In the other case, more challenging, the attacker can only access the inputs and outputs of the target model but not its internal confgurations. In this project we focused our attention on the black-box setting.

Frank Wolfe Variants

In this project my colleague and I focused on variants of Frank-Wolfe algorithm, in particular we implemented and tested the Zeroth-Order Stochastic Conditional Gradient Method (ZSCG) defined in Zeroth-order (Non)-Convex Stochastic Optimization via Conditional Gradient and Gradient Updates, Faster Zeroth-Order Frank-Wolfe Method (FZFW) and Faster Zeroth-Order Conditional Gradient Sliding Method (FZCGS) defined in Can Stochastic Zeroth-Order Frank-Wolfe Method Converge Faster for Non-Convex Problems?.

These variants are Zeroth-order algorithms because they do not use the gradient (like first-order methods) but a different criterion value based on the Frank-Wolfe criterion.

We tested the performance of these methods on the task of adversarial attack on black-box Deep Neural Network(DNN). The task was to find the universal perturbation δ such that the Deep Neural Network makes an incorrect classification. Following Can Stochastic Zeroth-Order Frank-Wolfe Method Converge Faster for Non-Convex Problems? we tested the algorithms with this loss function:

Results

Our results proved that the FZCGS algorithm has the highest convergence rate, while the ZCGS is the worst in terms of convergence. In the the github-repo there is the source code and the report with a long discussion on the experiments and final results.